Interactive Gridworld

What is a gridworld ?

A gridworld represents an environment in which an agent is able to take actions. The orange cell placed on the bottom right is the goal state, where we want to go. You can move the ending point by draging it. Walls have been placed and are represented by blue cells. You can place other ones by clicking or initiating a drag on an empty cell. Similarly, you can remove walls by clicking or initiating a drag on a wall cell.

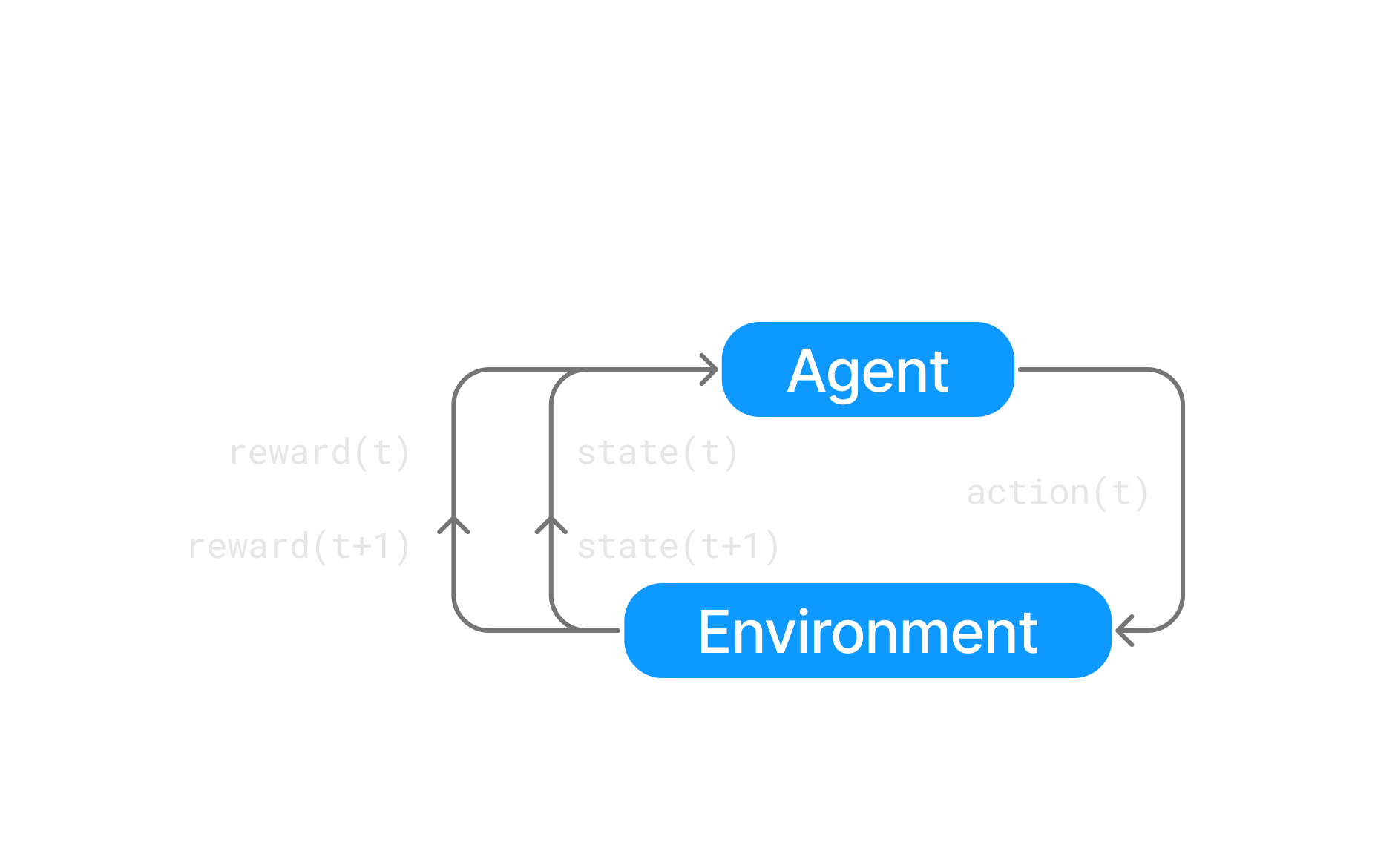
We start at the first time step on the starting point $s_0$, with an initial reward $r_0$ being $0$. At each time step $t$, we chose a possible action $a_t$. Let's say that we chosed to go down $a_0 = down$. If there is nothing or a wall, we get a 'reward' of $r_1 = -1$. And if we got to the end, we get a reward of $r_1 = +100$ and the game ends. Note that we can define a terminal state as a state where every action takes you to the same state with a reward of $0$. The goal is to finish the game with the maximum (discounted) reward possible $\sum_{t=0}^{+\infty} \gamma^t r_{t+1}$. That is why we give a negative reward when transitionning to a cell where there is nothing. This tells us that the shortest path to the end is going to be better than making 3 times the tour of the map before going to the goal state.
You might be wondering what this $\gamma$ thing is. It is a parameter between $0$ and $1$ called the discount factor. It indicates how much we care about rewards that are far in the future. If $\gamma$ is near $0$, we are going to take into account only reward in the near future. If, however, $\gamma$ is near $1$, we will considerate more long-lasting reward as well.

Markov Decision Process

You might also be wondering why we are defining the problem like this. That is because it is a very general way to define a problem where an agent is going to take actions in an environment. This is central to the field of Reinforcement Learning. The underlying mathematical model is called a Markov Decision Process. In this example, we will keep it simple and consider a deterministic MDP. In a deterministic MDP, the state you end up in after taking a certain action in a certain state is always the same. Another simplification we are going to make is that the reward you get when transitioning is independent of the action you took and only depends on the state you are transitioning to and the one you are transitiong from. Such an MDP is defined by:

• A set of states $S$
• A set of actions $A$
• A transition function $s: S \times A \rightarrow S$ that takes a state and an action and returns the next state
• A reward function $R: S \times S \rightarrow \mathbb{R}$ that takes a state and the next state and returns a reward

What is a policy, a state value and a Q-function ?

We first define the concept of policy. The policy is a function $\pi : S \rightarrow A$. In other words, it takes a state as an input and output an action to take. An agent is said to follow a policy $\pi$ if at every timestep $t$, $a_t = \pi(s_t)$ i.e. if it takes the action that the policy asks it to follow. We can now define what are a state-value and a Q-value (also called action-value) function given a policy:

$V^{\pi}(s_t)$ represents the future discounted reward, starting at $s_t$ and following the policy $\pi$. $Q^{\pi}(s_t, a_t)$ is very similar, it is the future discounted reward, still starting at $s_t$ but this time taking action $a_t$ (possilbly different from $\pi(s_t)$) before following the policy.

A policy which is going to maximize the future dicounted reward is called an optimal policy. There can be several ones sometimes (for instance if transitioning to nothing would yield a reward of 0 and if the discounting factor was 1) or if two paths from start to end have the same lengths. Let's take one, we are going to call it $\pi^*$, we also define the optimal state-value function $V^* = V^{\pi^*} = \max_{\pi} V^{\pi}$ as well as the optimal Q-value function $Q^* = Q^{\pi^*} = \max_{\pi} Q^{\pi}$. Note that all optimal policies share the same state-value and action-value (Q-value) function because if a policy was better than an optimal one, it would not be optimal.

Let's solve it !

The next remarks are going to be central for solving the problem, they are the Bellman Equations of a deterministic MDP (with deterministic policy).

By the same reasoning we obtain the equation for the action-value function:

For the optimal state-value and action-value functions, we have:

We can also remark that $V^*(s) = \max_a Q^*(s, a)$. This is because the maximum discounted reward from a state is the one that you would get by following the best action available in that state. We can now inject this in the equation:

This is called the Bellman Optimality Equation.

Code preliminaries

Those code examples are going to be written in Rust 🦀. We will be using a crate that I wrote for this purpose called madepro (for Markov Decision Processes). The code examples will be from the environment part of the library where the gridworld is defined. I will just show the part of the code that is relevant to the concepts we talked about. Some details like implementations of certain functions will be ommited as they are not relevant to the concepts we are talking about. We start by defining types to represent the gridworld and the different concepts we talked about:

Policy Iteration

The first method we are going to use is called Policy Iteration. We initialize the state-value function with a random one or we can also initialize it at $0$ for every state. We, then, derive a better policy from this state-value. We calculate the new state-value and again a new better policy, and so on until the policy is stable.

Policy Evaluation

We first need a method in order to estimate the state-value function of a policy. This technique is called Policy Evaluation. For this, we want to use the Bellman equation as an update rule for our state-value estimation:

We can then have two arrays, one for the old values and one for the new values calculated from the old ones. We can also do it in-place with one array, replacing values as we go through $S$. Although the latter is usually faster to converge, it is anisotropic in the sense that the order in which we are going to do the updates is going to matter. This example is from the implementation of the library [madepro][6].

Policy Improvement

Once we have evaluated the state-value function, we change our policy for a better one according to this state-value function:

Final Algorithm

Value Iteration

In Policy Iteration, we were estimating the state-value function of the policies until reasonable convergence. In Value Iteration, we instantly greedify the policy between the sweeps for state-value evaluation. It discards the need for actually computing the policy between each evaluation as it just computes the greedy one on the fly at the moment of choosing an action. In general, a variant of that algorithm is used where we do a few steps of evaluation between two policy improvement steps. In this case, the code will be the said variant.

Note that the implementation is shared between Policy Iteration and Value Iteration as they are very similar. The difference between the two is the iterations_before_improvement parameter of the Config object. It is used to do a few steps of evaluation before improving the policy in the case of Value Iteration. If it is set to None, we evaluate until convergence so the Policy Iteration algorithm is used.

Temporal Difference Learning

The last two methods we are going to look at are called SARSA and Q-Learning. They are both examples of Temporal Difference Learning. The idea is to estimate the state-value function by simulating episodes and updating the state-value function at each step. The advantage of these mehtods compared to dynamic programming methods like Policy Iteration and Value Iteration is that they can be used even in the case where the model is not known.

Exploration vs Exploitation

When simulating episodes in an environment, we need to balance between exploration and exploitation. One very simple way to do that is to take a random action with a certain probability $\varepsilon$ and the greedy action otherwise. The greedy action represents the exploitation of the current knowledge of the environment. The random action on the other hand represnets the exploration of the environment. Such a policy is called an $\varepsilon$-greedy policy.

Epsilon Greedy Policy

/// Returns a random action with probability epsilon
/// or the greedy action with probability 1 - epsilon.
pub fn epsilon_greedy<'a>(&'a self, actions: &'a Sampler<A>, epsilon: f64) -> &A {
    if random::<f64>() < epsilon {
        actions.get_random()
    } else {
        self.greedy()
    }
}

SARSA

With SARSA and $Q$-Learning we are going to be estimating $Q$ instead of $V$ and derive the optimal policy from it. Another difference with these methods is that we are going to be simulating episodes through the gridworld in order to estimate the $Q$-function instead of sweeping through the state space $S$. SARSA stands for State-Action-Reward-State-Action because we are going to look one action forward following the policy to estimate $Q(s,a)$.

Q-Learning

Q-Learning is basically the same as SARSA, it only differs in its update rule: instead of choosing a second action following the $\varepsilon$-greedy policy, we choose the best action available in the next state: $\argmax_{a'} a' \rightarrow Q(s', a')$

Remark that we do not completely update $Q(s,a)$ to the new computed value. We make a step in that direction of proportion $\alpha$, this parameter is the learning rate of our algorithm. It is used to make the algorithm more stable.

Final Note

If you want to see the actual code used here (TypeScript React), look here. Also, a lot of simplifications have been done in order to explain more directly the different concepts. Finally, we only looked at the case of deterministic MDP with known model. To have a better view of Reinforcement Learning, I recommend this excellent book about it written by Sutton & Barto, the visual representations from this article are actually directly inspired from that book but remade to fit this website colors.